Modern Genomics II

I cannot understand his accent...

• Contents that (I think) are important
  • Linkage disequilibrium (LD)
    • Coefficient of linkage disequilibrium ( D )
  • Relative measures of LD
  • Nucleotide diversity (\pi)
• Course contents according to recording

Contents that (I think) are important

Linkage disequilibrium (LD)

Coefficient of linkage disequilibrium \( D \)

Given two loci \(A\) and \(B\) (can have allele \(A\) or \(a\), \(B\) or \(b\)), the coefficient of linkage disequilibrium \(D\) is defined as

\[ D = \frac{P_{AB} - P_A P_B}{P_A P_B} \]

Below shows two examples of \(D\) calculation.

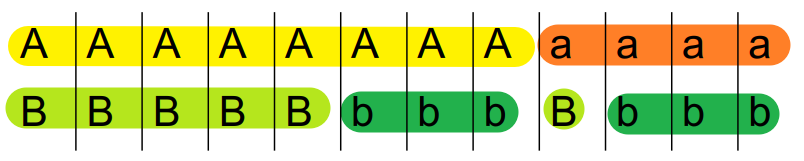
\[ D = \frac{P_{AB} - P_{A} P_{B}}{P_{A} P_{B}} = \frac{5}{12} - \frac{8}{12}\times\frac{6}{12} = \frac{1}{12} \]

A and B are linked to some extent.

\[ D = \frac{P_{AB} - P_{A} P_{B}}{P_{A} P_{B}} = \frac{6}{12} - \frac{8}{12}\times\frac{9}{12} = 0 \]

Here A and B are not linked at all.

Basically we are testing whether P(A) and P(B) are independent.

Relative measures of LD

1. \(r^2 = \frac{D}{P_A P_a P_B P_b}\)
2. \(D' = \frac{D}{D_{\max}}\) if \(D\) is positive, \(D' = \frac{D}{D_{\min}}\) if \(D\) is negative

Nucleotide diversity \(\pi\)

Average proportion of pairwise differences between the sequences

Give a multiple sequence alignment, \(\pi\) is defined as

\[ \pi = \sum_{i < j} \frac{\pi_{ij}}{n_c} \]

where \(n_c = \frac{n(n-1)}{2}\) is the number of pairwise comparisons, and \(\pi_{ij}\) is the proportion of differences between the \(i\)th and \(j\)th sequences.

Below shows an example of \(\pi\) calculation.

\[ \pi = \sum_{i < j} \frac{\pi_{ij}}{n_c} = \frac{\pi_{12} + \pi_{13} + \pi_{23}}{3} = 0.2 \]

Basically just calculating the average number of differences in the matrix.

Course contents according to recording

Title: Applications of next-generation sequencing and other genomic techniques

1. Resequencing to identify genetic basis of phenotypic variation
   1. Outlier approach
   2. Genome-wide association studies (GWAS) and linkage disequilibrium
2. Introduction to RNA-seq (transcriptome) focusing on genome duplication
3. Resequencing to detect signature of selection: nucleotide diversity

Microbial community and metagenomics, ChIP-seq, epigenomics, whole genome assembly as reference

• Evolutionary functional genomics can...
  • identify ecologically relevant genes
  • inferring selection & population processes